m-way search tree
앞 게시글에서는 계속해서 Binary 트리에 대해 다루었습니다.
06. 자료구조론 - 이진탐색트리 (Binary Search Tree)
이진탐색트리 (BST) 이진탐색트리는 이진트리의 일종으로, 트리의 노드들을 일정한 기준으로 정렬해놓아서 트리 내에서 원하는 노드를 쉽게 찾을 수 있도록 한 트리입니다. 이진탐색트리는 다음
coldyun.tistory.com
이진트리는 자식이 많아봐야 두개밖에 없기때문에 탐색 등의 연산을 빠르게 수행할 수 있습니다.
하지만 이진트리는 데이터베이스와 같이 디스크에 데이터를 저장하는 용도로 사용하기에는 적합하지 않은 자료구조입니다.
모든 데이터가 메인메모리에 들어있을 수는 없기 때문에 일부 데이터는 외부 디스크에 저장됩니다. 이때 디스크에 접근하는 것은 메인메모리에 접근하는 것보다 훨씬 느립니다.
그리고 디스크는 여러 개의 구역 (blocks, pages) 으로 나뉘어 있고, 구역 내의 특정 부분을 접근하는 것과 해당 block 전체를 접근하는 것은 동일한 시간이 걸립니다.
따라서 디스크에서 데이터를 가져올 때 시간을 줄이기 위해서는 디스크에 한번 접근해서 가져오는 데이터의 양을 늘리고, 디스크에 접근하는 횟수를 줄여야합니다.
이렇게 하기 위해서는 트리의 각 노드를 좀 더 넓게 만들어야합니다.
m-way search tree는 한 노드에 연결될 수 있는 자식노드를 최대 m개 까지로 늘린 트리입니다. (따라서 이진탐색트리는 2-way search tree와 같습니다.

degree: m, height: h인 트리에서
1. 노드의 최대 개수 = $(m^{h+1} - 1) / (m-1)$ ($m^0 + m^1 + m^2 + ... + m^h$)
2. 트리에 들어갈 수 있는 element의 최대 개수 = $m^{h+1} - 1$ (각 노드에 최대 m-1개의 element가 들어갈 수 있으므로)
B-Tree
order m을 갖는 B-tree는 다음의 특성을 만족하는 m-way search tree입니다.
1. 루트노드는 최소 2개의 자식을 갖는다.
2. 각 노드는 최대 m-1개의 키를 갖는다.
3. 모든 external 노드 (leaf 노드, 자식이 없는 노드)는 모두 같은 레벨에 있다. (perfectly balanced)
4. 루트노드를 제외한 모든 internal 노드는 $\lceil m/2 \rceil$과 m개 사이의 자식을 갖는다.
ex) m = 3일 때, 비트리의 모든 internal 노드는 2 또는 3개의 자식을 갖는다.
height h를 갖는 B-tree에서
1. 가장 좋은 케이스는 모든 internal 노드가 m개의 자식을 가지며 넓게 펼쳐져있는 트리입니다.
이 경우, 노드의 개수 $n = m^{h+1}-1$ 이 되고, 정리하면 $h = \lceil log_m(n+1) \rceil = O(log n)$이 됩니다. (m은 상수이므로)
2. 가장 나쁜 케이스는 모든 internal 노드가 $\lceil m/2 \rceil$개의 자식을 갖는 경우로,
$log_{\lceil m/2 \rceil}n = {log n \over {log \lceil m/2 \rceil}} = O(log n)$ 가 됩니다.
따라서 비트리에서는 어떤 경우에도 $h = O(log n)$을 만족합니다.
비트리 노드는 다음과 같이 구현할 수 있습니다.
#define ORDER 3
typedef struct _Node {
int size; // 자식 노드의 개수
struct _Node *child[ORDER]; // 자식노드에 대한 포인터배열
int key[ORDER-1]; // 노드에 들어가는 element들
}Operations
B-tree에서 search, insert, delete 연산이 어떻게 이루어지는지 알아보겠습니다.
Search
- $k_1 < k_2 < ... < k_{m-1}$의 key를 갖는 노드에 도달하면, 해당 key 배열에서 원하는 값 x를 찾습니다. (순차 탐색, 이진 탐색 등 어떤 방법으로든)
- 만약 x가 그 안에 존재한다면 완료
- x가 존재하지 않는다면, $k_i < x < k_{i+1}$을 만족하는 i를 찾아서 $p_i$가 가리키는 노드에 대해 위의 과정을 반복합니다.
- 시간 복잡도 : $log m \cdot log n = O(log n)$
- ($log m$은 1번 과정의 시간복잡도이고, 이를 최대 $O(log n)$ 번 반복하므로)
Insert
우선 새로운 값의 범위에 맞는 적합한 leaf 노드를 찾습니다.
- 만약 여기서 leaf 노드가 꽉 차있지 않다면, 해당 key를 해당 노드에 insert합니다.
- 만약 노드가 꽉 차있다면, 다음 중 하나의 방식을 통해 트리를 조정해야합니다.
- key rotation (sibling 노드에 자리가 남는 경우)
- node split (sibling 노드에도 자리가 없는 경우)
찾은 Leaf 노드에 빈 자리가 있는 경우입니다.
👉빈 자리에 바로 넣어줍니다.
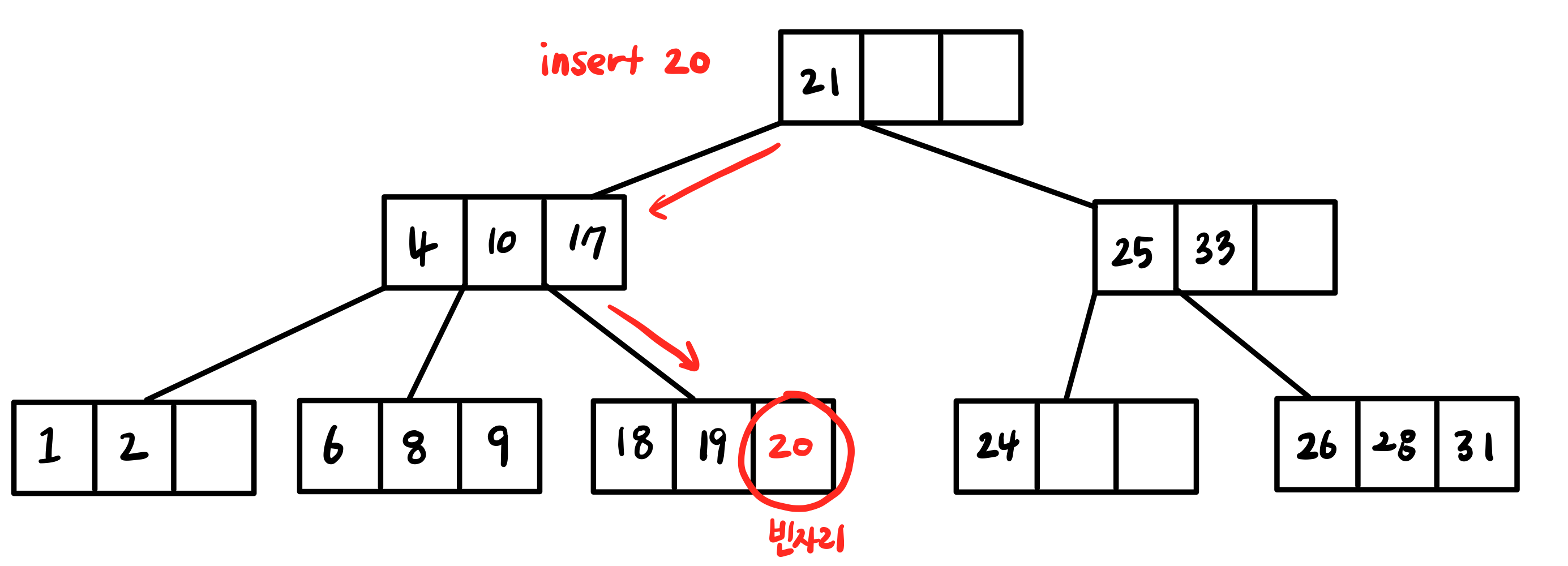
찾은 Leaf 노드에는 빈 자리가 없지만 Sibling 노드에는 빈 자리가 있는 경우입니다.
👉Key Rotation

1. 부모노드의 키를 sibling 노드의 빈 자리로 옮기고
2. 꽉 찬 노드에서 새로운 값을 포함하여 가장 작은 (또는 가장 큰)key를 부모노드로 옮기면,
새로운 값을 위한 자리가 하나 생기게 됩니다.
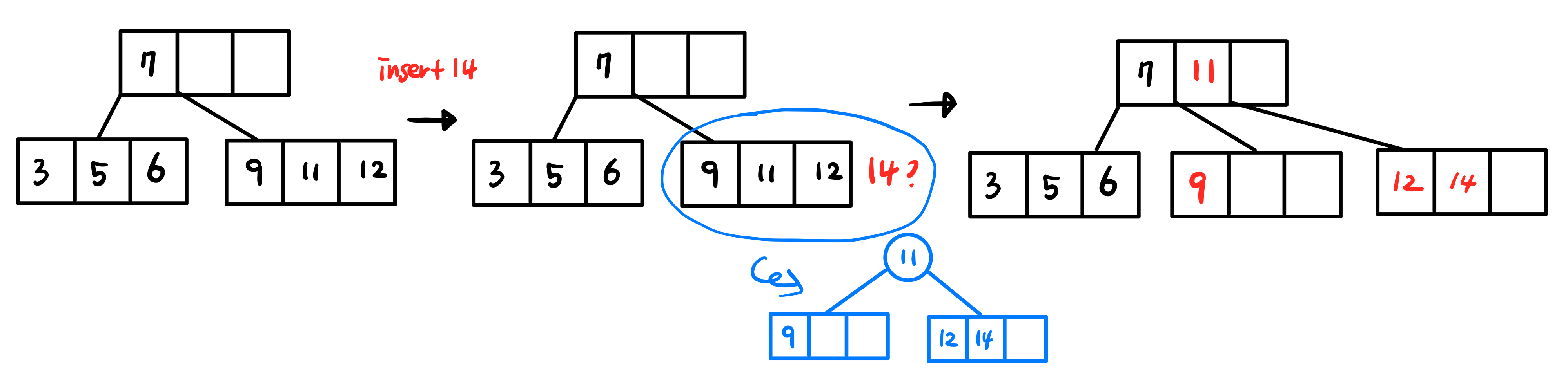
찾은 Leaf 노드에도 빈 자리가 없고 Sibling 노드에도 빈 자리가 없는 경우입니다.
👉Node Split
아무 곳에도 키들을 옮겨넣을 공간이 없다면, Leaf 노드를 3개의 노드로 쪼개야합니다.
- middle key를 가지는 노드
- middle key보다 작은 값을 가지는 key들을 위한 노드
- middle key보다 큰 값을 가지는 key들을 위한 노드
middle key는 아무 값이나 상관없지만 배열에서 중간 값을 가지는 key로 설정하는 것이 좋습니다.
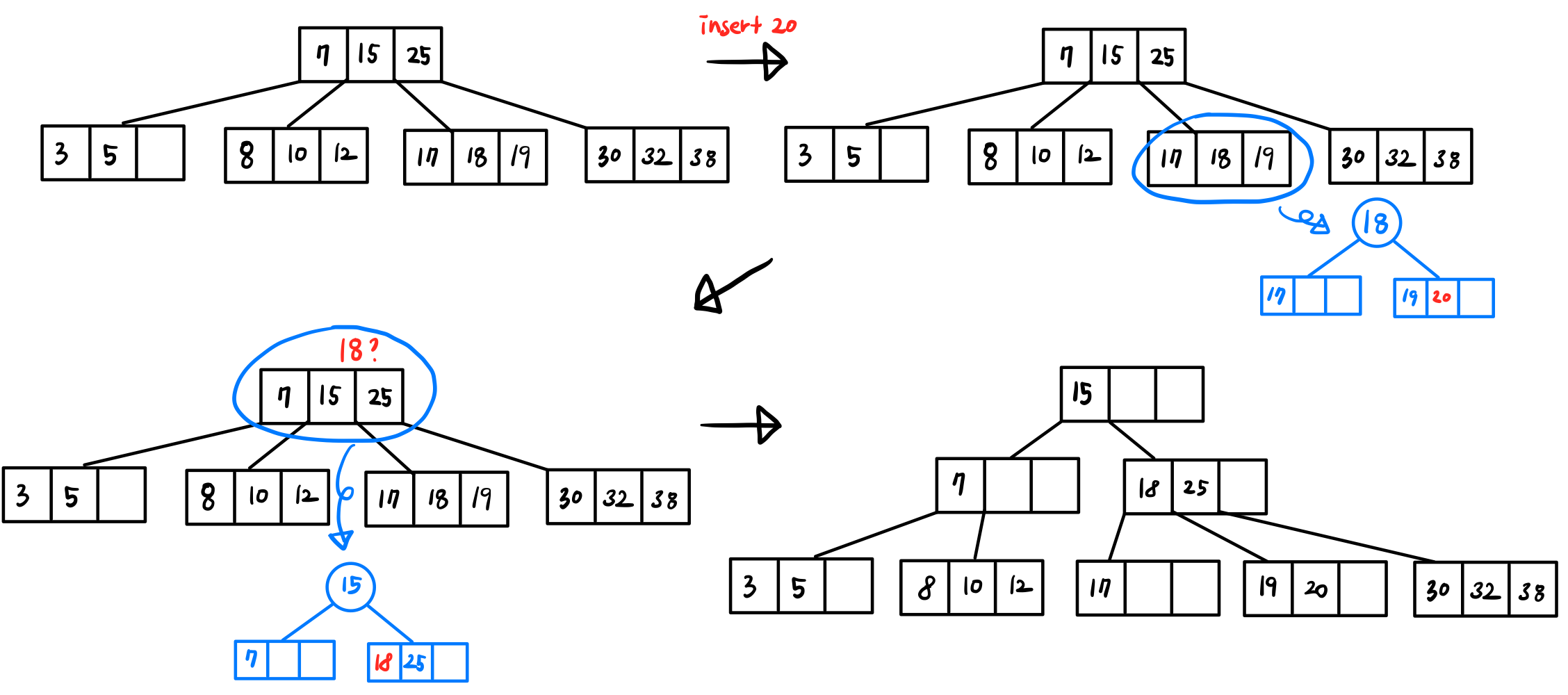
- 2번과 3번노드를 새롭게 생성하고, 1번의 middle key를 부모노드에 삽입합니다. 2번과 3번 노드는 부모에 삽입된 1번노드의 왼쪽과 오른쪽에 연결합니다.
- 만약 부모노드에 1번 노드를 삽입하면서 또다시 overflow가 난다면 Key rotation 또는 Node split 과정을 반복합니다.
- 만약 루트노드에서 overflow가 난다면, 2개의 자식을 가지는 새로운 루트노드를 만듭니다.
Delete
key가 하나만 있던 노드에서 delete가 일어나면서 <$\lceil m/2 \rceil$과 m개 사이의 자식이 존재>해야 한다는 b-tree의 조건이 깨지면 트리에 조정이 필요합니다.
- 다시 빈 곳을 채우는 방법으로는 key rotation 방법이 있습니다.
- 왼쪽 자식에서 가장 큰 key (혹은 오른쪽 자식에서 가장 작은 key)를 가져와 빈칸을 채우거나,
- 부모노드에서 key를 가져와 채우고 부모노드는 다른 자식 노드(처음 delete가 일어난 노드 기준 sibling노드)에서 key를 가져와 빈 부분을 다시 채우는 방법이 있습니다.
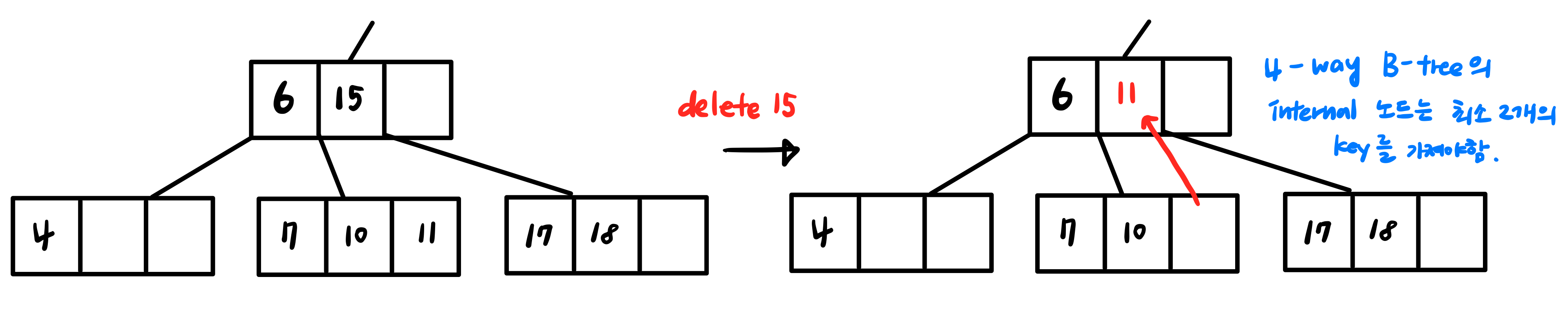

- 하지만 만약 자식 노드나 sibling 노드에 빌려줄 key가 부족하다면 두 노드를 합치는 node merging 방법을 사용할 수 있습니다.

이렇게 m-way B-tree를 이용하여 디스크에서 원하는 페이지를 찾을 때,
- 디스크 접근 횟수는 $O(log_m n)$번 이 됩니다.
이것은 트리의 height에 비례하는 것이고, m이 커질수록 디스크에 접근해야하는 횟수는 줄어들게 됩니다. 또한
- 각 디스크 접근마다 어떤 하위 노드를 선택해야하는지 결정하기 위해 $O(log m)$ 만큼의 오버헤드가 들게됩니다.
하지만 이 오버헤드는 메인메모리에서 수행되기 때문에 무시할 수 있습니다.
m-way에서 m은 보통 32에서 256 사이의 값으로 결정되며, 충분히 클수록 디스크에 접근하는 횟수는 줄어들지만, 하나의 internal 노드가 하나의 disk block에 들어갈 수 있을 만큼은 되어야합니다. 따라서 디스크의 데이터를 잘 관리하기 위해 적절한 m을 선택하는 것이 중요합니다.
'자료구조론' 카테고리의 다른 글
| 12. 자료구조론 - Dijkstra's algorithm (0) | 2023.01.30 |
|---|---|
| 11. 자료구조론 - Graph(1) Intro, Topological Sort (0) | 2022.06.27 |
| 09. 자료구조론 - Heap (Priority Queue) (0) | 2022.06.23 |
| 08. 자료구조론 - Disjoint Set (0) | 2022.06.22 |
| 07. 자료구조론 - AVL Tree (0) | 2022.06.22 |



